接續昨天的内容，今天我們來聊一聊邏輯回歸的數學原理。

邏輯回歸的原理

1. 線性組合：
   我們一開始説到，邏輯回歸就是想辦法用一條直綫將數據一分爲二，假設輸入特徵為X = [x_1, x_2, ... , x_n]，對應的權重為W = [w_1, w_2, ... , w_n]，模型會首先計算特徵的線性組合（這部分跟綫性回歸一模一樣）：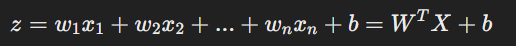
   
   其中，b是偏置項（bias）。

2. 使用 sigmoid 函數：
   由於線性組合的輸出範圍是正無窮到負無窮，我們需要將其轉換為一個 0 到 1 的範圍來表示概率。這就使用了 sigmoid 函數，其公式為：
   
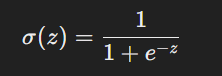
   這個 sigmoid 函數會將輸出的數值映射到(0, 1)區間，代表某一類別的概率。當概率大於某個閾值（通常是 0.5）時，我們可以將其分類為Class 1，否則為Class 2。

3. 決策邊界（Decision Boundary）：
   邏輯回歸的決策邊界是根據概率的閾值來確定的，當P(y=1 | X) > 0.5時，模型將輸出 1 類別，否則輸出 0 類別。由於邏輯回歸的 sigmoid 函數會產生一個 S 形曲線，因此它的決策邊界是線性的，適合處理線性可分的數據集。

4. 損失函數（Loss Function）：
   在訓練過程中，邏輯回歸使用對數損失（Log Loss）或稱為 交叉熵 （Cross-entropy）來優化模型。對數損失函數定義如下：
   
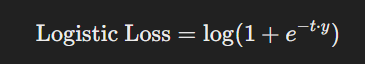
   其中：

   • t是模型預測的輸出（通常是線性組合t = W^T * X + b）。
   • y是真實標籤，通常取值為+1或-1。

   目標是通過調整權重 W 和偏置 b，使得損失函數最小化。

邏輯回歸的目標

邏輯回歸的目標是將輸入特徵 ( X ) 的線性組合 ( z = W^T X + b ) 映射為 0 到 1 之間的概率值，這樣我們就可以預測某事件發生的概率。

令 P(y = 1 | X)代表事件發生（即 ( y = 1 )）的概率，而P(y = 0 | X) 則代表事件不發生（即 ( y = 0 )）的概率。這兩者之間的關係為：P(y = 0 | X) = 1 - P(y = 1 | X)
因此，我們需要找到一個函數能夠將輸入的線性組合 ( z ) 轉換為事件發生的概率。

使用 odds 和 log-odds

為了解釋概率和線性組合之間的關係，我們引入賠率（odds）的概念，賠率定義為事件發生的概率和不發生的概率的比率：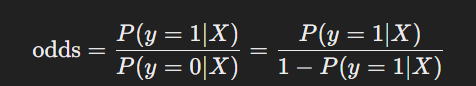

然後我們對賠率取對數，得到對數賠率（log-odds）：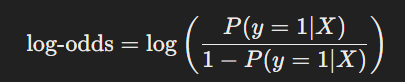

邏輯回歸假設對數賠率與輸入特徵的線性組合 ( z ) 呈線性關係，即：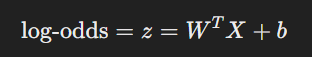

這是邏輯回歸的核心假設之一，表明線性組合 ( z ) 可以解釋為對數賠率。